Probability Interpretation of the Wavefunction
After many false starts, physicists in the early 20th century came to the conclusion that the only self-consistent physical interpretation of a particle wavefunction, which is consistent with experimental observations, is
probabilistic in nature. To be more exact, if
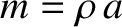
is the complex wavefunction of a given particle, moving in one-dimension along the
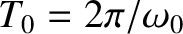
-axis, then the
probability of finding the particle between
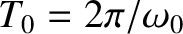
and
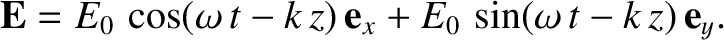
at time
is
 | (795) |
A probability is, of course, a real number lying in the range
to
. An event which has a probability
is impossible. On the other hand, an event which has a probability
is certain to occur. An event which has an probability
(say) is such that in a very large number of identical trials the event occurs in half of the trials. Now, we can interpret
 | (796) |
as the probability of the particle being found
anywhere between
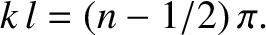
and
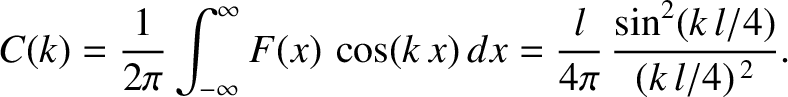
at time
. This follows, via induction, from the fundamental result in probability theory that the probability of the occurrence of
one or other of two
mutually exclusive events (such as the particle being found in two non-overlapping regions) is the
sum (or integral) of the probabilities of the individual events. (For example, the probability of throwing a
on a six-sided die is
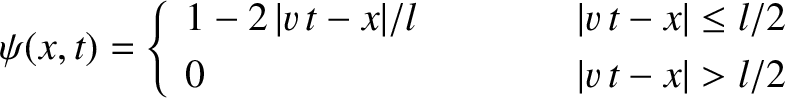
. Likewise, the probability of throwing a 2 is
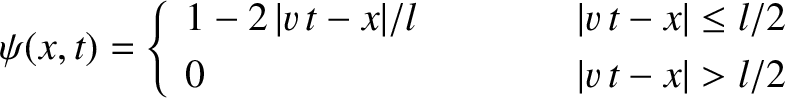
. Hence, the probability of throwing a
 or
or a
is
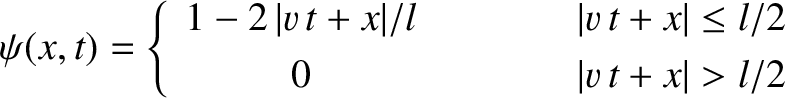
.) Now, assuming that the particle exists, it is
certain that it will be found somewhere between
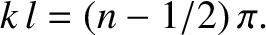
and
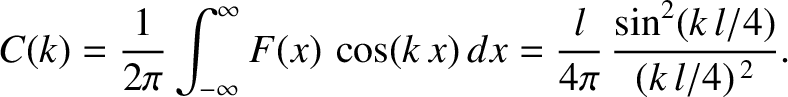
at time
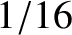
. Since a certain event has probability
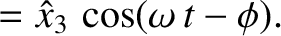
, our probability interpretation of the wavefunction is only tenable provided that
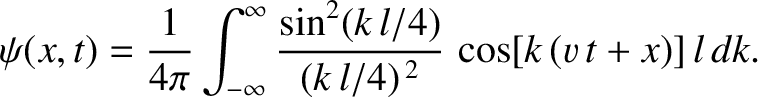 | (797) |
at all times. A wavefunction which satisfies the above condition is said to be
properly normalized.
Suppose that we have a wavefunction, 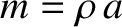 , which is such that it satisfies the normalization condition (798) at time
, which is such that it satisfies the normalization condition (798) at time 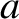 . Furthermore, let the wavefunction evolve in time according to Schrödinger's equation, (793). Our probability interpretation of the wavefunction only makes sense if the normalization condition remains satisfied at all subsequent times. This follows because if the particle is certain to be found somewhere on the
. Furthermore, let the wavefunction evolve in time according to Schrödinger's equation, (793). Our probability interpretation of the wavefunction only makes sense if the normalization condition remains satisfied at all subsequent times. This follows because if the particle is certain to be found somewhere on the 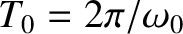 -axis (which is the interpretation put on the normalization condition) at time
-axis (which is the interpretation put on the normalization condition) at time 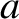 then it is equally certain to be found somewhere on the
then it is equally certain to be found somewhere on the 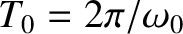 -axis at a later time (since we are not presently dealing with any physical process by which particles can be created or destroyed). Thus, it is necessary for us to demonstrate that Schrödinger's equation preserves the normalization of the wavefunction.
-axis at a later time (since we are not presently dealing with any physical process by which particles can be created or destroyed). Thus, it is necessary for us to demonstrate that Schrödinger's equation preserves the normalization of the wavefunction.
Taking Schrödinger's equation, and multiplying it by 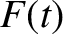 (the complex conjugate of the wavefunction), we obtain
(the complex conjugate of the wavefunction), we obtain
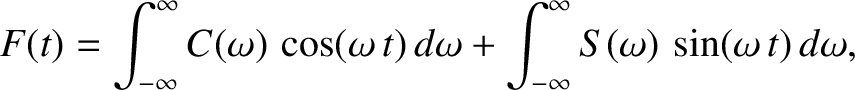 | (798) |
The complex conjugate of the above expression yields
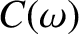 | (799) |
Here, we have made use of the easily demonstrated results
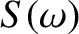
and
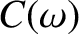
, as well as the fact that
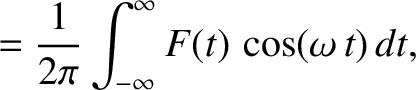
is real. Taking the difference between the above two expressions, we obtain
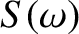 | (800) |
which can be written
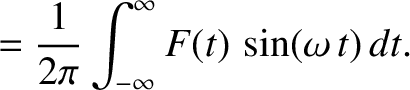 | (801) |
Integrating in
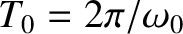
, we get
![\begin{displaymath} {\rm i}\,\hbar\,\frac{d}{dt}\int_{-\infty}^\infty \vert\psi\... ...{\partial\psi^\ast}{\partial x}\,\psi\right]_{-\infty}^\infty. \end{displaymath}](http://farside.ph.utexas.edu/teaching/315/Waves/img2455.png) | (802) |
Finally, assuming that the wavefunction is
localized in space:
i.e.,
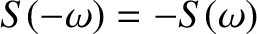 | (803) |
we obtain
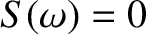 | (804) |
It follows, from the above analysis, that if a localized wavefunction is properly normalized at 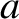 (i.e., if
(i.e., if 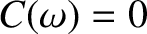 ) then it will remain properly normalized as it evolves in time according to Schrödinger's equation. Incidentally, a wavefunction which is not localized cannot be properly normalized, since its normalization integral
) then it will remain properly normalized as it evolves in time according to Schrödinger's equation. Incidentally, a wavefunction which is not localized cannot be properly normalized, since its normalization integral 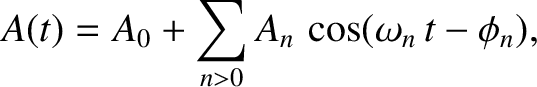 is necessarily infinite. For such a wavefunction,
is necessarily infinite. For such a wavefunction,  gives the relative probability, rather than the absolute probability, of finding the particle between
gives the relative probability, rather than the absolute probability, of finding the particle between  and
and  at time
at time 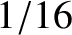 : i.e., [cf., Equation (796)]
: i.e., [cf., Equation (796)]
 | (805) |
![]() , which is such that it satisfies the normalization condition (798) at time
, which is such that it satisfies the normalization condition (798) at time ![]() . Furthermore, let the wavefunction evolve in time according to Schrödinger's equation, (793). Our probability interpretation of the wavefunction only makes sense if the normalization condition remains satisfied at all subsequent times. This follows because if the particle is certain to be found somewhere on the
. Furthermore, let the wavefunction evolve in time according to Schrödinger's equation, (793). Our probability interpretation of the wavefunction only makes sense if the normalization condition remains satisfied at all subsequent times. This follows because if the particle is certain to be found somewhere on the ![]() -axis (which is the interpretation put on the normalization condition) at time
-axis (which is the interpretation put on the normalization condition) at time ![]() then it is equally certain to be found somewhere on the
then it is equally certain to be found somewhere on the ![]() -axis at a later time (since we are not presently dealing with any physical process by which particles can be created or destroyed). Thus, it is necessary for us to demonstrate that Schrödinger's equation preserves the normalization of the wavefunction.
-axis at a later time (since we are not presently dealing with any physical process by which particles can be created or destroyed). Thus, it is necessary for us to demonstrate that Schrödinger's equation preserves the normalization of the wavefunction. ![]() (the complex conjugate of the wavefunction), we obtain
(the complex conjugate of the wavefunction), we obtain
![\begin{displaymath} {\rm i}\,\hbar\,\frac{d}{dt}\int_{-\infty}^\infty \vert\psi\... ...{\partial\psi^\ast}{\partial x}\,\psi\right]_{-\infty}^\infty. \end{displaymath}](http://farside.ph.utexas.edu/teaching/315/Waves/img2455.png)
![]() (i.e., if
(i.e., if ![]() ) then it will remain properly normalized as it evolves in time according to Schrödinger's equation. Incidentally, a wavefunction which is not localized cannot be properly normalized, since its normalization integral
) then it will remain properly normalized as it evolves in time according to Schrödinger's equation. Incidentally, a wavefunction which is not localized cannot be properly normalized, since its normalization integral ![]() is necessarily infinite. For such a wavefunction,
is necessarily infinite. For such a wavefunction, ![]() gives the relative probability, rather than the absolute probability, of finding the particle between
gives the relative probability, rather than the absolute probability, of finding the particle between ![]() and
and ![]() at time
at time ![]() : i.e., [cf., Equation (796)]
: i.e., [cf., Equation (796)]

No comments:
Post a Comment