| (i) In example 8.1.6, the basis S={(1, 1, 1, ), (-1, 0, -1), (-1, 2, 3)} of 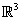 gave the orthonormal basis gave the orthonormal basis
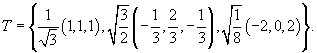
(ii) Consider the vector space V = 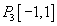 of all real-polynomial function p(x), of all real-polynomial function p(x), 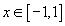 ,of ,of
degree at most 3. Let the inner-product on V be given by
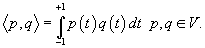
Consider the basis S = 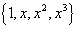 for V. for V.
The Gram-Schmidt process gives the following.
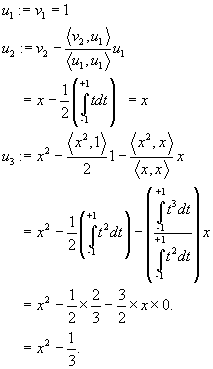

Next, define
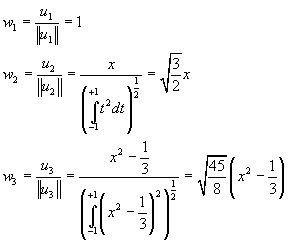
Then 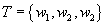 is an orthonormal basis of V. is an orthonormal basis of V.
(iii) Let W denote the subspace of 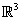 spanned by the set of vectors: spanned by the set of vectors:
S = {(1, 1, 1), (2, 2, 3), (0, 0, 1), (1, 2, 3)}.
Clearly S is not a basis of W , since S has four elements. Thus, to find an orthonormal basis of W one
way is to first select a basis of W out of the vectors in S and then apply Gram-Schmidt process to it.
Another, more straight forward method, is to apply Gram-Schmidt process directly to the set
of vectors in S , and discard those vectors which become zero.
In our case it is as follows:
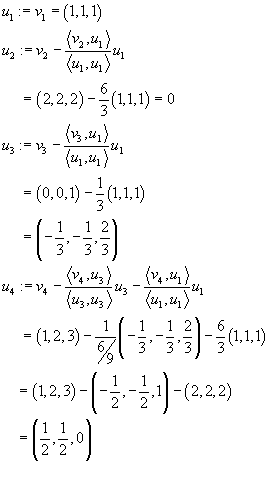
The required orthonormal basis is
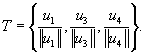 |
No comments:
Post a Comment