Contains the syllabus(organic,physical and inorganic chemistry),notes,guidelines and solutions of Msc Chemistry 1st year and 2nd year run by Tribhuvan University ,Institute of Science and Technolgy.Nepal.
Wednesday, April 6, 2011
Ph.D. In TU
Requirements for Admission in M.Sc Degree
Course offered in Msc Chemistry TU
Course offered for masters degree in Chemistry (M,Sc.) are of two years duration. The total mark in theory and labaratory works in M.Sc first part is 500. Similarly the total mark in theory, laboratory work and /or dissertation in M.Sc second part in 500. During second year session,students may choose an area of specialization in one of the three streams: Physical Chemistry, Organic Chemistry and Inorganic Chemistry while in first year all students are in one general stream. In total ,there are 180 students are studying in the Department.
Similarly Trichandra college also has chemistry department . With 150 students studying ata the moment both in first year and second year.
Tuesday, April 5, 2011
Central Department of Chemistry TU Tribhuvan University Nepal
1.To produce high skilled manpower with MSc. and PhD degrees
2.To promote research activities in Chemistry and related fields.
3.To improve and upgrade the Chemistry curricula of The University of different levels in accordance to the national requirements and maintaining the international standards.
4.To conduct postdoctoral researches.
5.To promote relations with various national and international institutions concerned with Chemistry.
6.To develop relations between chemistry related governmental and n0n-governmental organizations.
7.To provide consultancy services in various areas of Chemistry.
MSc Chemistry In Tribhuvan University (TU),Kritipur
Masters Degree programs in inorganic and Physical Chemistry was introduced in 1966 and 1976 respectively. Late Prof. Dr. Dhurba Man Singh Amatya was formally appointed as the first head of the department in 1966 and he remained to that post upto 1984.After Prof. Amatya Prof. Dr. S.P.Dhoubhadel,Prof.Dr.C.L.Gajurel,Prof.J.K Shrestha,Prof.Dr.M.D Manandhar and Prof. Dr. R.R Pradhananga became the heas of department during the period between 1984-2007. Dr. Tulasi Pathak leaded the department since November 13,2007.Prof. Dr. K.N.G is head of Department these days....
Monday, April 4, 2011
Radio Chemistry
General radio chemistry: The term radio chemistry first introduced in 1910 by A.G Cameron . It may defined as branch of science which delas with the study of the nature and properties of radioactive elements and their products. F. Paneath defined radio chemistry as the chemistry of the substances that are studies by their radiations . It is now defined as the branch of chemistry which deals with the study of radioactive isotopes elements and substances. The laws of their physio chemical behavior ,the chemistry of nuclear transformations and associated physio -chemical processes.
Types of radio chemistry
There are four major types of radio chemistry
1.General radio chemsitry
2.Chemistry of nuclear transformation
3.chemistry of radioactive element
4.applied chemistry
1. General radio chemsitry
This deals with the study of physico-chemical laws that govern the behaviour of radioactive isotopes and elements. Radio active the elements and isotopes are mostly prepares and used in quantities that are inaccessible weighing. The natural abundance of radioactive isotopes are extremely low.
a. Isotope exchange reactions :
When two substances having an atom or ion come together in a uniform submission or along the ....
Nuclear Chemistry-Elective Course-Msc 2nd year
Course content by topics:
1,Nucleonics
2.Nuclear Reactions
3.General radio chemistry
4.Hot atom Chemistry
5. Radiation Chemistry
6.Radiation Biology
Question Module:
1. Comprehensive Question
4 out of 6 each carrying 10 marks
2. Short questions
7 out of 9 each 5 marks
Saturday, April 2, 2011
Notes of msc chemistry.
msc in trichandra college
msc chemistry tu
Msc Chemistry Tribhuvan University Old questions.
MSc Chemistry Syllabus T.U
MSc Chemistry in Nepal
Chemistry syllabus of Master of Science in Chemistry of Tribhuvan University
I hope it will be useful to many of us.
Thanks
MSc Chemistry Frst year Course Structure.
Subjects Course Number Full Marks Pass Marks
Inorganic Chemistry: Chem 511 100 40
Physical Chemistry: Chem 512 100 40
Organic chemistry :Chem 513 100 40
Research Methodology: Chem 514 100 40
Inorganic Chemistry Practical Chem :515 100 40
Physical Chemistry Practical Chem :516 100 40
Organic chemistry Practical Chem :517 100 40
#Submission of a term paper in research methodology course is a prerequisite to appear in the first year final examination
Friday, April 1, 2011
The Born-Oppenheimer Approximation
The Born-Oppenheimer Approximation
The Born-Oppenheimer Approximation is the assumption that the electronic motion and the nuclear motion in molecules can be separated. It leads to a molecular wave function in terms of electron positions  and nuclear positions
and nuclear positions  .
.

This involves the following assumptions
- The electronic wavefunction depends upon the nuclear positions
 but not upon their velocities, i.e., the nuclear motion is so much slower than electron motion that they can be considered to be fixed.
but not upon their velocities, i.e., the nuclear motion is so much slower than electron motion that they can be considered to be fixed. - The nuclear motion (e.g., rotation, vibration) sees a smeared out potential from the speedy electrons.
...................................................................................................
The Born-Oppenheimer approximation
The forces on both electrons and nuclei due to their electric charge are of the same order of magnitude, and so the changes which occur in their momenta as a result of these forces must also be the same. One might, therefore, assume that the actual momenta of the electrons and nuclei were of similar magnitude. In this case, since the nuclei are so much more massive than the electrons, they must accordingly have much smaller velocities. Thus it is plausible that on the typical time-scale of the nuclear motion, the electrons will very rapidly relax to the instantaneous ground-state configuration, so that in solving the time-independent Schrödinger equation resulting from the Hamiltonian in equation 2.12, we can assume that the nuclei are stationary and solve for the electronic ground-state first, and then calculate the energy of the system in that configuration and solve for the nuclear motion. This separation of electronic and nuclear motion is known as the Born-Oppenheimer approximation .
Following Ziman [7], we assume the following form of an eigenfunction for the Hamiltonian (2.12):
| (2.18) |
in which the dependence of the eigenvalues
The energy
 | |||
![$\displaystyle - \sum_{\gamma} \int \prod_{\beta} {\mathrm d}{\bf r}_{\beta} \Ph... ...la}_{\gamma} \Psi \left( \{ {\bf r}_i \} ; \{ {\bf r}_\alpha \} \right) \right]$](http://www.tcm.phy.cam.ac.uk/%7Epdh1001/thesis/img70.gif) |
and the term in square brackets can be rewritten
 |  | ||
| (2.21) |
since the normalisation of the electronic wave-function does not change when the nuclei move, so that the first order contribution vanishes. The second-order shift due to this term does not vanish and gives rise to transitions between electronic states as the ions move, otherwise known as the electron-phonon interaction, which will modify the energy.
The second non-adiabatic term in the final term of equation 2.20 will be largest when the electrons labelled ![]() are tightly bound to the nuclei labelled
are tightly bound to the nuclei labelled ![]() in which case
in which case ![]() where
where ![]() and the first order correction from this term is
and the first order correction from this term is
![$\displaystyle ~- \int \prod_j {\mathrm d}{\bf r}_j \prod_{\beta} {\mathrm d}{\b... ...\right) \nabla_{\gamma}^2 \Psi \left( \{ {\bf u}_{(i,\alpha)} \} \right) \Bigr]$](http://www.tcm.phy.cam.ac.uk/%7Epdh1001/thesis/img77.gif) | |||
![$\displaystyle - \sum_{\gamma} \frac{1}{2 m_{\gamma}} \left[ \int \prod_{\beta} ... ...right) \nabla_{\gamma}^2 \Psi \left( \{ {\bf u}_{(i,\alpha)} \} \right) \right]$](http://www.tcm.phy.cam.ac.uk/%7Epdh1001/thesis/img78.gif) | |||
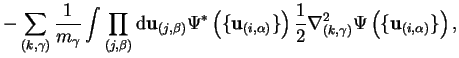 | (2.22) |
and this quantity is of the order of the electronic kinetic energy multiplied by the ratio of the electron and nuclear masses, typically a factor of the order of
We therefore neglect the non-adiabatic terms and note that equation 2.20 is satisfied if ![]() obeys a Schrödinger equation of the form
obeys a Schrödinger equation of the form
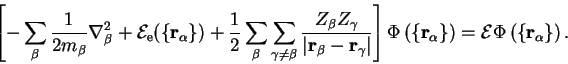 | (2.23) |
This adiabatic principle is crucial because it allows us to separate the nuclear and electronic motion, leaving a residual electron-phonon interaction. From this point on it is assumed that the electrons respond instantaneously to the nuclear motion and always occupy the ground-state of that nuclear configuration. Varying the nuclear positions maps out a multi-dimensional ground-state potential energy surface, and the motion of the nuclei in this potential can then be solved. In practice Newtonian mechanics generally suffices for this part of the problem2.7, and relaxation of the nuclear positions to the minimum-energy configuration or molecular dynamics [11,12] can be performed. These aspects go beyond the scope of this dissertation so that from now on it is assumed that a system with a fixed nuclear configuration is to be treated, so that the electronic energy ![]() is a constant and the electronic wave-function
is a constant and the electronic wave-function ![]() obeys the Schrödinger equation 2.19. The dependence of the electronic wave-function on the nuclear positions
obeys the Schrödinger equation 2.19. The dependence of the electronic wave-function on the nuclear positions ![]() is now suppressed.
is now suppressed.
The Born-Oppenheimer Approximation
The next few lectures will treat the problem of quantum chemistry, a subfield of quantum mechanics also known as molecular quantum mechanics. The idea of quantum chemistry is to use only the simple facts molecules and, indeed, all of ordinary matter, can be viewed as composed only of positively charged nuclei and negatively charged electrons. This universal description is then subject to a quantum mechanical treatment from which the properties of the system are derived or computed.
We begin our discussion of AIMD by considering a system of ![]() nuclei described by coordinates,
nuclei described by coordinates, ![]() , momenta,
, momenta, ![]() , and masses
, and masses ![]() , and
, and ![]() electrons described by coordinates,
electrons described by coordinates, ![]() , momenta,
, momenta, ![]() , and spin variables,
, and spin variables, ![]() . The Hamiltonian of the system is given by
. The Hamiltonian of the system is given by
where
If we sought to solve the complete quantum mechanical problem, we start by seeking the eigenfunctions and eigenvalues of this Hamiltonian, which will be given by solution of the time-independent Schrödinger equation
where
The Born-Oppenheimer (named for its original inventors, Max Born and Robert Oppenheimer) is based on the fact that nuclei are several thousand times heavier than electrons. The proton, itself, is approximately 2000 times more massive than an electron. In a dynamical sense, the electrons can be regarded as particles that follow the nuclear motion adiabatically, meaning that they are ``dragged'' along with the nuclei without requiring a finite relaxation time. This, of course, is an approximation, since there could be non-adiabatic effects that do not allow the electrons to follow in this ``instantaneous'' manner, however, in many systems, the adiabatic separation between electrons and nuclei is an excellent approximation. Another consequence of the mass difference between electrons and nuclei is that the nuclear components of the wave function are spatially more localized than the electronic component of the wave function. In the classical limit, the nuclear are fully localized about single points representing classical point particles. Thus, it follows that the nuclear wave function rises more steeply than the electronic wave function, which means that ![]() , from which we may approximate
, from which we may approximate
| (3) | |||
![$\displaystyle -{\hbar^2 \over 2}\sum_{I=1}^N {1 \over M_I} \left[\psi({\bf x},{... ...f R}) + 2\nabla_I\psi({\bf x},{\bf R})\cdot\nabla_I\phi({\bf x},{\bf R})\right]$](http://www.nyu.edu/classes/tuckerman/quant.mech/lectures/lecture_10/img33.png) | |||
 | (4) |
Substitution of Eq. (2) into Eq. (1) and using the approximation that the nuclear wave function ![]() is more localized than the electronic wave function, i.e.
is more localized than the electronic wave function, i.e. ![]() , yields
, yields
| (5) |
Eq. (6) is an electronic eigenvalue equation for an electronic Hamiltonian,
Moreover, each electronic eigenvalue,

The Born-Oppenheimer surfaces are surfaces on which the nuclear dynamics is described by a time-dependent Schrödinger equation for the time-dependent nuclear wave function ![]() :
:
An important assumption of the Born-Oppenheimer approximation is that there are no excitations of the electrons among the various surfaces. Such excitations constitute non-adiabatic effects which are, therefore, neglected. As an example of a conditions in which this approximation is valid, consider a system at temperature ![]() . If the electrons are in their ground state
. If the electrons are in their ground state ![]() , then, if
, then, if ![]() denotes the first excitates state, there will be no excitations to this state if
denotes the first excitates state, there will be no excitations to this state if
| (9) |

In many cases, non-adiabatic effects can be neglected, and we may consider motion only on the ground electronic surface described by:
Moreover, if nuclear quantum effects can be neglected, then we may arrive at classical nuclear evolution by assuming
| (11) |
which is just the classical Hamiltonian-Jacobi equation with
denoting the classical nuclear Hamiltonian. The Hamilton-Jacobi equation is equivalent to classical motion on the ground-state surface,
Note that the force
Equations (14) and Eq. (15) form the theoretical basis of the AIMD approach. The practical implementation of the AIMD method requires an algorithm for the numerical solution of Eq. (14) with forces obtained from Eq. (15) at each step of the calculation. Moreover, since an exact solution for the ground state electronic wave function,

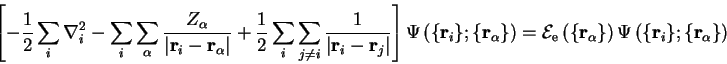
![$\displaystyle {\hat H} {\tilde \Psi} \left( \{ {\bf r}_i \} , \{ {\bf r}_\alpha... ...rt} \right] {\tilde \Psi} \left( \{ {\bf r}_i \} , \{ {\bf r}_\alpha \} \right)$](http://www.tcm.phy.cam.ac.uk/%7Epdh1001/thesis/img65.gif)
![$\displaystyle \quad= \Psi \left( \{ {\bf r}_i \} ; \{ {\bf r}_\alpha \} \right)... ... {\bf r}_{\gamma} \right\vert} \right] \Phi \left( \{ {\bf r}_\alpha \} \right)$](http://www.tcm.phy.cam.ac.uk/%7Epdh1001/thesis/img66.gif)
![$\displaystyle \qquad - \sum_{\beta} \frac{1}{2 m_{\beta}} \Bigl[ 2 {\bf\nabla}_... ...bla_{\beta}^2 \Psi \left( \{ {\bf r}_i \} ; \{ {\bf r}_\alpha \} \right) \Bigr]$](http://www.tcm.phy.cam.ac.uk/%7Epdh1001/thesis/img67.gif)

![$\displaystyle \frac{\left[T_{\rm e} + V_{\rm ee}({\bf r}) + V_{\rm eN}({\bf r},{\bf R})\right] \phi({\bf x},{\bf R})} {\phi({\bf x},{\bf R})}$](http://www.nyu.edu/classes/tuckerman/quant.mech/lectures/lecture_10/img40.png)


